教案二重积分的计算教学内容重积分的计管早多元积分学的其木技术也是多重积分以及曲面积分的计

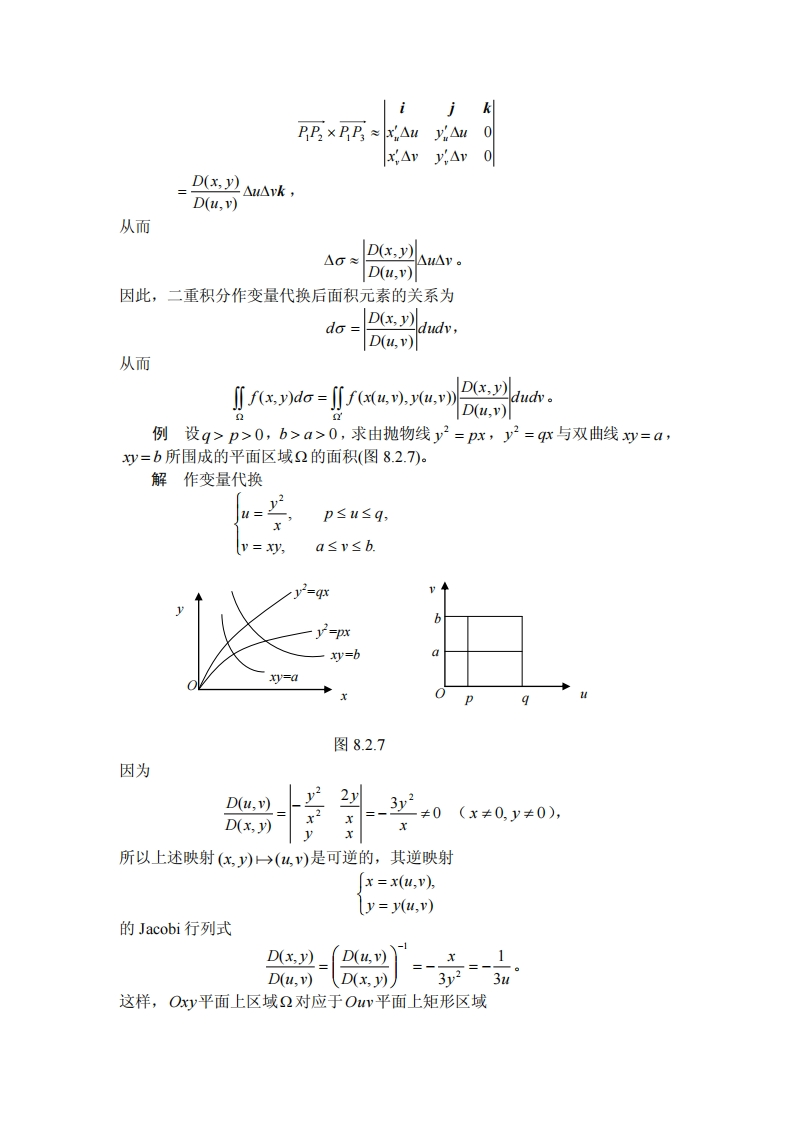
散案二重积分的计算教学内容二重积分的计算是多元积分学的基本技术，也是多重积分以及曲面积分的计算的基础，是微积分的重要工具之一。在这节中主要讲解以下几方面的内容：(1)直角坐标系下二重积分的计算：(2)二重积分的变量代换法：(3)极坐标系下二重积分的计算。教学思路和要求(1)计算重积分的基本思路是将重积分化为累次积分，通过逐次计算定积分，求得重积分的值。讨论二重积分的计算，其途径即是化二重积分为二次积分。通过“已知平行截面面积，求空间区域体积”的背景，引入二重积分化为二次积分来计算的方法，可以给学生一个直观上的认识。(2)回忆定积分换元法的思想，可以对二重积分换元法则加深理解。注意指出作变量代换后面积元素的比例系数是Jacobi行列式的绝对值。(3)从直角坐标到极坐标的变量代换是二重积分计算中十分常见的代换。当区域边界或被积函数易于用极坐标表示时，采用极坐标往往能带来很大的便利。因此这部分的内容还是要重点强调。(4)有必要向学生介绍实例计算时的思考方法，引导他们提高计算能力。教学安排一.直角坐标系下二重积分的计算首先，假设区域Ω可表示为2={(x,y)川p(x)≤y≤p2(x),a≤x≤b。我们将根据二重积分的几何意义把∬fao化为二次积分。为此，暂且假设f≥0。由上一节可知，∬fdo的值等于2=x,y)以2为底，以曲面z=f(x,y)为顶的曲顶柱体的体积V(图8.2.1)，这个体积实际上还可以用一元函数积分学中“已知平行截面面积，求空间区域体积”的方法来求得。为此，我们固定x∈[a,b],过(x,0,0)且平行于Oyz的平面截曲项柱体得到的截面d6是该平面上一个以区间[p(x),p2(x)]为下底，z=f(x,y)为曲边的一个曲图8.2.1边梯形，所以这个截面面积为40)=x.